LIMITES DE FUNCIONES
DESCRIPCION:
Una función f tiene un límite L en
el punto c, significa que el
valor de f puede ser tan cercano a L como
se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.
EJERCICIO:
APLICACIONES:
Los arquitectos utilizan los límites de una función para saber el
crecimiento de una colonia en la cual se va a trabajar; y el trabajo que éste
desempeñará, al construir una vivienda más por cada habitante que se integre.
Además se la ocupa si se va
a construir una obra en la que debes realizar aproximaciones con un margen de
error mínimo debes usar límites.
Algunos números irracionales
como "e" que no se pueden obtener mediante una ecuación algebraica se
pueden escribir de manera perfecta usando límites.
Ejemplo
e=lim(1+1/n)^n cuando n tiende a infinito.
LIMITES UNILATERALES
DESCRIPCIÓN:
Definición de límite por la derecha |
|
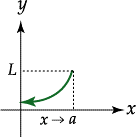
Podemos observar que cuando nos acercamos por la derecha con las x al valor de a, los valores de la función se van acercando a L
|
Observe que no hay barras de valor
absoluto alrededor de x-a, pues x-a es mayor que cero
ya que x>a.
Definición de límite por la izquierda
|
|
El concepto de limite por la izq es
completamente similar al limite por la derecha, solo que la variable x se
acerca al valor a por la izquierda, es decir, con valore que son menores a A
Note que la expresión a-x es mayor que cero,
pues x↦ a (elevado a la -1) por
lo que x <a.
EJERCICIO:
Determinar los límites de la función " f " definida por:
Primero hagamos la gráfica de la función:
El punto de discontinuidad se presenta
cuando x=1
Luego:
Observe que el límite por la derecha (3), es diferente al límite por la
izquierda (2).
APLICACIONES:
En la Arquitectura sirve
para elaborar gráficas que ayudan a saber el nivel de producción que se
obtendrá, encontrando el menor costo posible para generar una mayor ganancia.
Porque los clientes siempre necesitan saber un costo aproximado del nuevo
diseño que el arquitecto crea.
Además permite calcular velocidades
y aceleraciones (razones de cambio)
LIMITES INFINITOS
DESCRIPCION:
El símbolo ∞, se lee infinito, es de carácter posicional, no representa ningún
número real.
Si una variable independiente x está creciendo indefinidamente a través de valores positivos, se
escribe x ↦ +∞ (que se lee: x tiende a más infinito), y si decrece a través de valores
negativos, se denota como x ↦ -∞ (que se lee: x tiende a
menos infinito).
EJERCICIO
Ahora observe que es "x" la que tiende a
tomar valores positivos cada vez mayores, obteniendo como resultado que f "x" tiende a valores
cercanos a cero.
Así lim x ↦ +∞ f(x)↦ 0 ,
o sea, f(x)↦ 0 cuando x ↦ +∞.
APLICACIONES:
Se lo aplica cuando hacemos cálculos con medidas de
tiempo y otros campos que no son finitos
CONTINUIDAD EN UN PUNTO
DESCRIPCION:
La
continuidad significa que un pequeño cambio en la variable X implica sólo un
pequeño en el valor de f(x), es decir, la gráfica consiste de un sólo trozo de
curva.
Una
función f(x) es continua en un punto a si lim x->a f(x)
= f(a).
Nota: observar que debe existir f(a) y debe existir el limx->a f(x) y debe ser igual a f(a).
|
|
f(x)= 1/x2
Discontinua en x=0 (No existe f(0)) |
EJERCICIO:
La función es
continua en todos los puntos de su dominio.
D = R− {−2,2}
La función tiene dos puntos de discontinuidad en x
= −2 y x = 2.
APLICACIONES:
En cualquier
lugar del universo, por ende en la naturaleza y en la vida diaria, aparecen numerosos fenómenos
que tienen un comportamiento continuo. Por ejemplo: el crecimiento de una planta es continuo, el desplazamiento de
un vehículo o el volumen del agua que
fluye de un recipiente, el movimiento planetario y una infinidad de otros
eventos.
CONTINUIDAD EN UN INTERVALO
DESCRIPCION:
Una función f(x) es continua en un intervalo cerrado
[a, b] si: f es continua en x, para todo x perteneciente al
intervalo abierto (a, b).
f es continua en a por la derecha:
f es continua en b por la izquierda:
EJEMPLO:
f(x) es continua por la izquierda en x = 0 ,
ya que f(x)= x2 por
ser una función polinómica es continua en toda R.
f(x) es
continua por la derecha en x = 4 , ya que f(x) = 4 por ser una función
polinómica es continua en toda R.
Para que f(x)
sea continua en todos los puntos del intervalo (0, 4) tenemos que estudiar la
continuidad en el punto x = 2, que es el único dudoso por tratarse de una
función definida a trozos.
f(2)= 4
Por tanto f(x) es continua en el intervalo [0,
4].
APLICACIONES:
En
la arquitectura se utiliza en la continuidad de un intervalo en las:
Deformaciones
de vigas
Diseño
de estructuras de puentes
Momentos
de estructuras de vigas columnas, losas
VIDEO DE INTRODUCCIÓN A LIMITES
NOTA: Todos estos temas se los pueden utilizar en los cálculos para ARQUITECTURA TRADICIONAL y ARQUITECTURA MODERNA
BIBLIOGRAFIA